By Josh Cosford, Contributing Editor
Pascal’s Law, a fundamental principle of fluid power, explains how pressure in an enclosed fluid is uniformly transmitted to move and support loads.
Sometimes, we fluid power professionals can’t see the forest for the trees. We take for granted the first-day education we experienced in college or university that provided the foundation for everything in this fluid power forest we thrive within. Every one of you didn’t know the difference between pressure drop and back pressure before you were taught, and to be honest, there are less than well-trained fluid power professionals who still do not.

Blaise Pascal, often referred to as the father of fluid power.
If you’re reading this, you’re either a fluid power professional or a neophyte looking to become one. Any foundation starts with a solid base, and many subjects such as geometry, pressure drop and symbology fill the bottom of the fluid power knowledge pyramid. A critical buttress in the foundation of knowledge is Pascal’s Law.
I try to write using accessible and colloquial verbiage, except when I use pretentious phrases such as colloquial verbiage. Nevertheless, Pascal’s Law is a beautiful discovery that never fails to illicit wows from those reading about it in textbooks or pushing interconnected syringes to operate a fluid power challenge device.
The origins of fluid power
Pascal’s Law explains the very nature of the hydrostatic force that holds mass and moves loads. Named after the French mathematician and physicist Blaise Pascal, the law states that “pressure applied to an enclosed fluid is transmitted undiminished to all areas of the fluid and at perpendicular vectors to the walls of its container.” Okay, maybe that description is more advanced than elementary, so let’s break it down.
Imagine you are seated on a cork that is plugging a giant, water-filled flask (Figure 1 – yep, that’s you). That cork presses down on the water with a force intensity factored by both the surface area of the cork and your slender mass (or swole mass – whatever you’re going for). Because this is an elementary discussion, we’ll also discuss the pressure triangle (Figure 2).
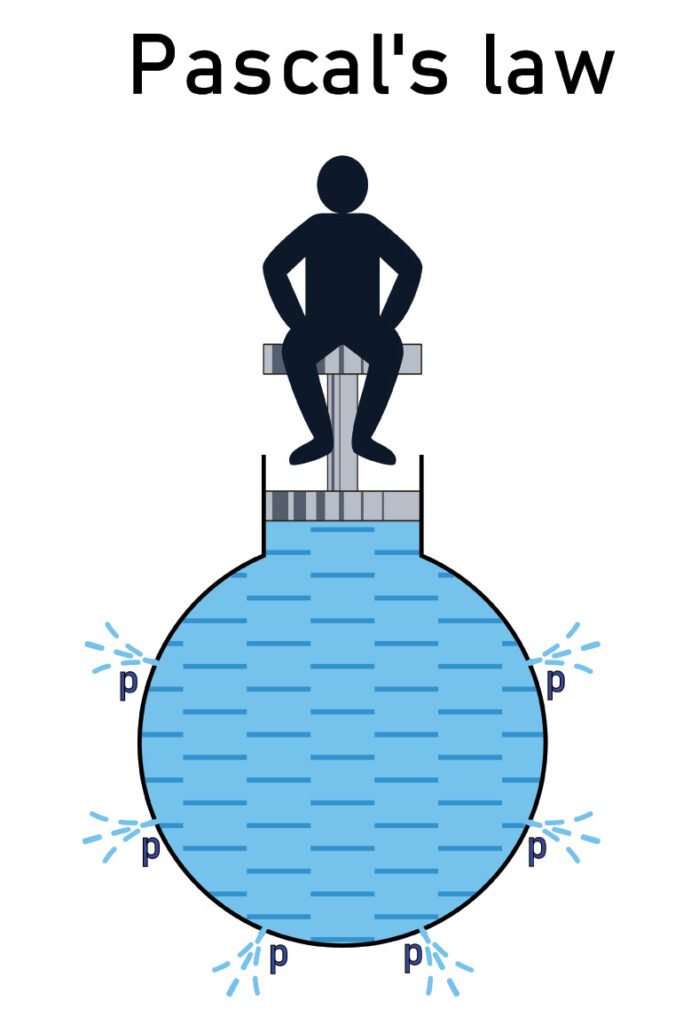
Figure 1. Illustration shows the basics of Pascal’s Law — when an external force acts on a liquid in a container, the pressure in the liquid is the same everywhere.
Using the triangle, you can arrive at Force, Area or Pressure by following the mathematical direction of the other two variables. For example, multiply Pressure by Area if you want to calculate Force. If you want to determine Pressure, divide Force by Area. For example, if we apply 3,000 psi by an area of 12.56 in.2, we arrive at 37,680 lb of force.
Returning to your precarious perch atop the giant water flask, let’s assume your body weight is a lean 200 lb from your years of CrossFit. Your chair/piston/cork happens to be constructed from tungsten, weighing 99,800 pounds and machined to 20 in. diameter at the base. You’ll notice I said diameter, yet the FPA Triangle requires area.
The area of importance is the bottom surface of the chair/piston/cork, for which we use the trusty formula of πr2 to calculate how many square inches make up the circle. Expanded, the formula is Pi x (radius squared), so we must first calculate the radius. The radius of a circle is exactly half its diameter, so we’re talking about 10 in. Pi is a non-terminating decimal rounded frequently to 3.14. Putting it together, we write it out as A = 3.14 x 102 = 314 in.2 (remember to square the radius as the first step).
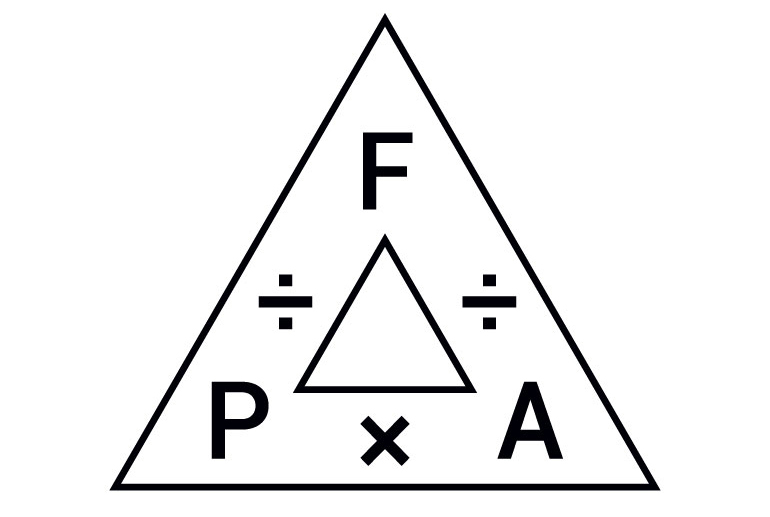
Figure 2. Pressure, force and area formula triangle
Back to the FPA Triangle, we’re calculating pressure, so we must divide the force by area. The force is the combined 100,000 lb from you and your chair/piston/cork, and the area is 314 in.2 Thus, 100,000/314 = 318.5 pound per square inch (psi). In hydraulic terms, 319 psi is relatively low, but stop to think about pressure, and if it helps, get a ruler and draw a 1-in. by 1-in. square on a piece of paper. That one square has more than your body weight pressing down upon it, and now expand your imagination to include 314 of those squares exerting the same force.
The power of the cylinder
I’ll remind you again of Pascal’s law: “Pressure applied to an enclosed fluid is transmitted undiminished to all areas of the fluid and at perpendicular vectors to the walls of its container.” Our flask is indeed enclosed, and pressure is applied by you and your chair/piston/cork. For the purposes of this discussion, the pressure exists equally at every spot in that flask, although if the flask were ocean-deep, its water’s mass would result in higher pressure at the bottom. But let’s ignore that for now.
What’s often misunderstood is how the force only acts at right angles to the pressure surface. The pressure your chair/piston/cork applies is straight down, and the opposing pressure vector is straight up. Regarding our circular flask, the pressure acts only at right angle radii to each infinitely small angle.
The primary reason circular shapes are so strong under pressure is the diffuse direction force acts upon its walls. Conversely, a cube has six flat surfaces for which pressure is unified against each surface. Even just a few psi inside a sealed reservoir can turn it into a barrel shape. However, nearly every shape used in fluid power is cylindrical — hoses, ports, spools, cylinder pistons, pump pistons, etc.
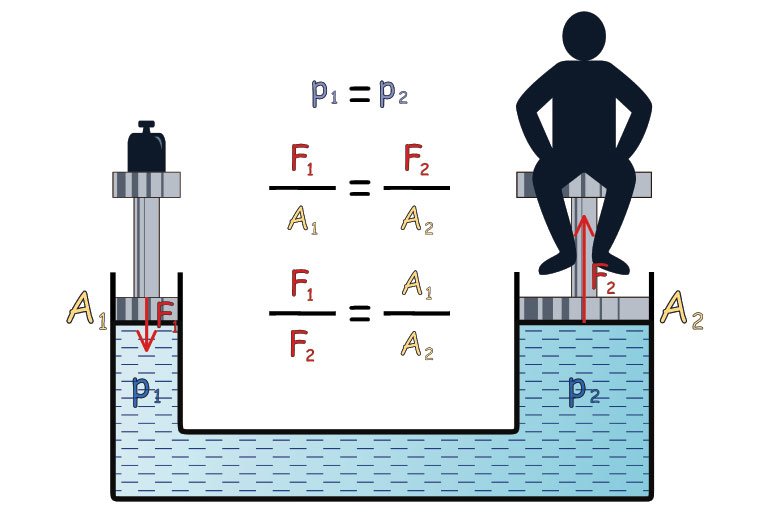
Figure 3. The calculation of pressure in a hydraulic device and graphical representation and application of Pascal’s law using a weight and a person.
There is little practical purpose in perching on the flask, so expect to ask passersby if they dig your tungsten chair/piston/cork. So long as the outside diameter of the tungsten piston area remains sealed with the inside diameter of the flask stem, you’ll effectively float as the mass above is equalized by the pressure below.
The real fun begins when you open the flask to other shapes. Imagine you now take two containers joined by a channel. You sit atop your chair/piston/cork, and your combined 100,000 lb still requires 318.5 psi to keep you from sinking because the system is no longer sealed. The channel ends at the other side with a similar, but smaller, cylinder with a small weight atop its chair/piston/cork (Figure 3).
Intuitively, you would expect there is no way the smaller weight on the smaller chair/piston/cork could do anything but shoot skyward as your combined weight drops you like a rock into your open cylinder. You might be surprised to learn you would actually rise higher as the small weight drops down. Let’s do some quick math to explain.
The smaller chair/piston/cork has a diameter of 10 in., and because we’re using exponents in our math, the surface area is much less than half the diameter. Using the same πr² that was previously discussed, we calculate the area as only 78.5 in.² We only need to use the FPA Triangle to calculate the force: 318.5 psi x 78.5 in.² = 25,002 lb.
So how does something that weighs 25,000 lb move something that weighs 100,000 lb? Well, that’s the magic of Pascal’s Law! You can’t get something for nothing, so what gives? The caveat is that the smaller weight has to move four units for every single unit of movement for you and the chair/piston/cork. For example, if the small weight moves four inches, you’ll only lift one inch. If you’re clever and paid attention in science class, then you know this not unlike a lever ratio.
In Figure 3, we show the math required to calculate these ratios. We know that P1 equals P2 — because of Pascal’s Law. The quotient of F1/A1 equals the quotient of F2/A2, or in simpler words, the equation works. If we bump the weight on the smaller chair/piston/cork to 26,000 lb, the math increases the pressure to 331 psi. Since your weight and the perch are “only” 100,000 lb, the 331 psi now working on the 314 in.² of your chair/piston/cork equates to 104,000 lb, easily raising you higher.
Pascal’s Law and hydraulics
If you allow me to expand your mind briefly, let’s zoom out and look at how these force ratio concepts apply to hydraulics. The smaller you make the piston for any given force input, the higher pressure it creates. The trade-off is that you need to move the smaller piston a farther distance equal to essentially the area advanced by the larger piston. Moving an area through distance creates volume; we can also look at this from that perspective.
In hydraulics, we prefer to work more quickly than can be achieved through the limited scale of Figure 3. Instead of pistons/chairs/corks, we use pumps, and quite small ones, relatively. Instead of area, we describe a pump by how much volume it creates in a single rotation, and then we spin those pumps at thousands of revolutions per minute. The surface area of any given vane, piston or gear on these pumps is a fraction of a square inch, showing you how something small can lift something big, but it’s actually the whole point.
Blaise Pascal made a discovery so monumental that his original tests and experiments must have triggered accusations of witchcraft. Without his discoveries, my life, your life and the life of every future fluid power professional may look vastly different. If you know a young fan of STEM, forward this article and allow them to take their first step into the magical forest we call fluid power.
Filed Under: Engineering Basics